Gradyanlar

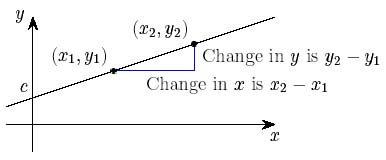
Şekil 1: Doğrunun gradyanı

Basit bir örnekle, yanda şekil 1'de gösterilen doğruyu düşünerek başlayalım. Doğrunun eğimi, $$\frac {\mbox{y'deki değişim}}{\mbox{x'deki değişim}}.                               (1)$$ olarak tanımlanır. Doğru üzerinde iki ayrı nokta $ (x_1, y_1) $ ve $ (x_2, y_2) $ alırsak gradyan aşağıdaki gibi tanımlanır:
$$m: = \frac {y_2-y_1} {x_2-x_1}.$$
Bu, hangi noktaları aldığımıza bağlı değildir. $ m $ 'yi bu şekilde tanımlarken doğrunun denklemi
$$y = mx + c$$ olur. Burada $ c $, doğrunun $ y $ ekseninden geçtiği noktanın $ y $ değeridir.

Fakat Şekil 2'de gösterilen $ x ^ 2 $ fonksiyonunun grafiği gibi düz olmayan eğrilerle ne yapmalıyız? $ x = 3 $ noktasını seçelim ve eğri için $ (3,9) $ noktasında bir gradyana sahip olmanın ne anlama geldiğine karar vermeye çalışalım. Yapacağımız şey bir "teğet" çizmek ve bu doğrunun gradyanını bulmak. Eğrinin gradyanı, bu doğrunun gradyanı olarak tanımlanacaktır. "Verilen noktada $ x ^ 2 $ fonksiyonuyla aynı gradyana sahip" bir doğru bulmaya çalışmakla korkunç bir dolambaçlı iddiaya giriyoruz. Ancak gradyanın ne olduğunu henüz bilmediğimizden problem yok! Bunun yerine, bir teğet çizgisinin ne olabileceği konusunda biraz fikir sahibi olmaya çalışalım.

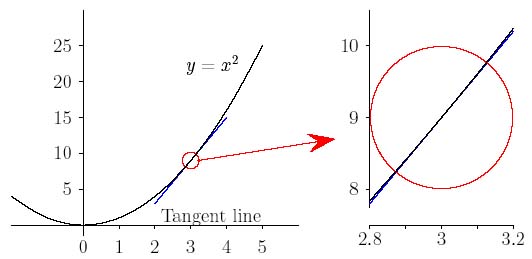Şekil 2: x = 3'de y = x² gradyanını bulma

Bundan böyle bir büyüteç veya mikroskobunuz olduğunu ve (3,9) noktasına yaklaştığınızı düşünün. (3,9) noktası etrafındaki fonksiyona daha yakından bakmak için yakınlaşmayı artırıp zum yaptığınızı düşünün. Bunu yaparsanız çok yakında eğri düzeliyor gibi görünür. Çok yüksek büyütmeler için $ x ^ 2 $ eğrisi aslında düz bir çizgiye benzer. (3,9) noktasında $ x ^ 2 $ fonksiyonunun büyütme altında düz olduğu anlaşılmaktadır. Dolayısıyla $ x ^ 2 $ 'un gradyanını, çok yüksek büyütme altında görülen düz çizginin gradyanı olarak $ x = 3 $' de tanımlamaya çalışıyoruz.

Yine de dikkat! Hem $ x $ hem de $ y $ yönlerini eşit ve aynı anda büyütmeniz çok önemlidir. Örneğin sürekli olarak $ x $ eksenlerini gererseniz fonksiyon sonunda düz gibi görünür! Bu çok yanıltıcıdır.

Zaten bildiğiniz üzere türev almanın formel süreci, bu gradyan değerini sadece (3,9) noktasında değil, büyütme altında düz bir halde olan bir fonksiyonun herhangi bir noktasında hesaplamamızı sağlar. Birazdan bir limit argümanını inceleyerek bir noktadaki $ x ^ 2 $ eğrisinin eğiminin $2x $ olduğunu göstereceğiz.

Aşağıdaki grafiğe göz atın. Bu çok karışık görünüyor, ancak büyütme altında da düz gibi görünüyor. $ x = 0,4246... $ civarındaki küçük bir alan yirmi kez büyütüldü. Aslında fonksiyonu daha da büyütürsek hemen yerel olarak düz gibi görünür ve bir teğet doğrusunun nasıl çizileceğine karar verebiliriz.

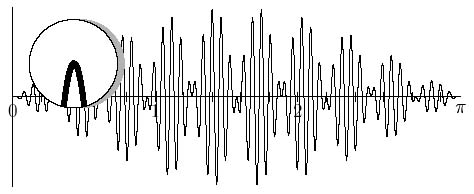Şekil 3: Aslında pürüzsüz olan ve hatta büyütme altında düz görünen "sarmal" bir fonksiyon

Dolayısıyla sadece grafiğin kendisine gelişigüzel bakmak, fonksiyonun büyütme altında düz olup olmadığı konusunda iyi bir kanıt değildir. Bununla birlikte polinomlar gibi yaygın olarak karşılaşılan birçok fonksiyon ve ayrıca $ \sin (x) $, $ \cos (x) $ ve $ e ^ x $ fonksiyonları büyütme altında düz görünecektir. Yaptığınız şeyi pek düşünmeden kalkülüsün formel kurallarını mekanik bir şekilde uygulamak tehlike ile doludur. Kalkülüsün bu kadar etkili olması ve kalkülüsün uygulanabileceği  fonksiyonların çokluğu, bazen tüm fonksiyonların büyütme altında düz olacağı düşüncesiyle insanı dikkatsizliğe çekebilir.