Enstrüman Yapım Sanatı

Çoğu enstrüman, şu iki titreşim biçiminden birini veya bunların bir kombinasyonunu kullanır: Yapı veya hava. Bir enstrümanı düşününce oldukça karmaşık bir etkileşim içinde olsa da muhtemelen kullanılan formları görebilirsiniz.

Örneğin, bir kemandan gelen ses başlangıçta yayın tellerin titreşmesini (yapısal) sağlamasından kaynaklanır ancak bu, titreşimin ahşap gövdeye (yine yapısal) aktarılmasıyla güçlendirilir. Bununla birlikte gövdenin şekli içerideki havanın titreşim şeklini etkileyerek sesin kalitesini (hava titreşimi) değiştirir.

Müzik enstrümanı yapma sanatı, doğal titreşim biçimlerinden yararlanmak üzere şekiller oluşturmaktan ve hava hacimlerini çevrelemekten gelir.

Doğal Frekanslar ve Müzik

Müzik aletleri, çoğu yapı ile ortak olarak paylaştıkları, bir dizi frekanstan birinde kolaylıkla titreştirilebilme özellikleri sayesinde bir ses üretebilirler. Diğer tüm frekanslarda bu büyük uğraş gerektirir. Doğal olarak yanıt verdikleri frekanslara doğal frekanslar denir ve titreşim sırasında deforme oldukları karşılık gelen şekillere modlar denir. Genellikle baskın olan ilk (veya en düşük) doğal frekanstır.

Bir nesneye vurursanız, doğal frekansında titreşmeye başladığı için oluşan bir ses duyarsınız. Bu, nesnenin şekli ve yapıldığı malzeme ile ilgilidir. Parmak eklemi ile bir masaya vurun ve ardından bir kitaba dokunun; daha yumuşak malzeme, daha düşük frekanslı bir ses çıkarır (her iki ses de ahşap ve kağıdın köreltici özelliğinden dolayı hızla kaybolur). Müzik aletleri, melodiye dönüşebilen hoş seslere neden olan malzemeler ve şekiller kullanarak bu fenomenden yararlanır.

Mbira: Afrika Piyanosu

Soldaki enstrüman bir mbira veya Afrika piyanosudur. İnce bir tahta veya plastik parçası yerine, yassılaştırılmış çelikten yapılmış kamışlara sahiptir. Bu kamışlar genellikle, gerekli tonu veren şekli elde etmek için becerinin gerekli olduğu yerlerde dövülmüş inşaat çivilerinden yapılır.

Mbira, Afrika'nın büyük bir bölümünde çalınır; şu anda Zimbabwe'de gece kulüplerinde ve CD'lerde ticari Afro-rumba müziği çalan bazı gruplar tarafından güçlendirilmiş biçimde kullanılmaktadır. Her biri belirli bir notayla ilişkilendirilmiş farklı kamışları görebilirsiniz. Geleneksel olarak bunlar, sakinleştirici, hafif hipnotik melodiler üreten döngüsel, ritmik bir modelde parmaklarla çalınır. Bu formda enstrüman dini törenlerde uygun bir atmosfer yaratmak için kullanılmıştır.

Matematiksel Modelleme

Bu titreşimlerin en basit matematiksel modeli, bir yay üzerinde titreşen bir kütleden gelir. Newton yasası, kuvvetin kütle çarpı ivme olduğunu söyler. İlk harekete geçirici kuvvet uygulandıktan sonra sadece yay, titreşimi etkiler. Hareket denklemi şöyle olur:

$$ku=m\frac{d^2u}{dt^2}$$

Burada u, kütlenin denge konumuna göre yer değiştirmesidir ve k ise yayın sertliğidir.

Gradyanlar 2

Bazı fonksiyonların grafiklerine büyütme altında bakıldığında düz olmadıkları görülür. Örneğin aşağıdaki şekilde tanımlı |x| fonksiyonu x=0 noktasında düz değildir:

Şekil 4: Farklı büyütmeler altında |x| grafiği

İkinci Dereceden Denklemlerin 100 Kullanımı: Uçuş

İkinci dereceden denklemler ile ikinci dereceden diferansiyel denklemler arasındaki bağlantı tesadüf değildir: hepsi Newton'un ikinci yasasında tanımlanan kuvvet ve ivme arasındaki bağlantıyla bağlantılıdır. Newton bu yasayı formüle ettiğinde esas olarak katı cisimlerin hareketini düşünüyordu. Bununla birlikte, su ve hava gibi sıvıların taşınması için de aynı yasaların uygulanabileceği kısa sürede fark edildi. Özellikle, bir sıvının hızı ile basıncı arasındaki ilişkiyi bulmak için Newton yasalarını kullanmak mümkündür. Bu yasaların (Navier-Stokes ve ilgili kısmi diferansiyel denklemler olarak adlandırılır) sofistike versiyonları hava durumunu tahmin etmek için büyük bilgisayarlarda çözülür. Bununla birlikte, birçok sıvı akışı tipi için geçerli olan belirli bir çözüm, uçuşun temel prensiplerinin keşfindeki anahtar bileşenlerden biriydi. Bunun sonuçları ölçülemezdi ve (her zamanki gibi) Bernouilli denklemi olarak adlandırılan ikinci dereceden bir denklemle bağlantılıdır.

İkinci Dereceden Denklemlerin 100 Kullanımı: Newton - 2

Bir bilgisayar kullanarak böyle denklemlere yaklaşık çözümler bulmak mümkündür ve bu genellikle modern teknolojide karşılaşılan çok karmaşık diferansiyel denklemler için kullanılan yaklaşımdır. Ancak matematikçi Leonhard Euler, ikinci dereceden bir denklemin çözümüne dayanan bu özel denklemi çözmenin bir yolunu tasarladı. Euler, $$x(t)=e^{wt}$$ formunun bir çözümünün varlığını önerdi. Bu fonksiyonun önemi ise şudur: $$\frac{de^{wt}}{dt}=we^{wt}.$$Diferansiyel denkleme yerleştirip $e^{wt}$ ile bölersek $w$ değişkenli aşağıdaki denklemi buluruz:$$aw^2+bw+c=0.$$Bu çok tanıdık! Orijinal diferansiyel denklemi çözmek için tek yapmamız gereken bu ikinci dereceden denklemi çözmek ve $w$ yerine geri koymaktır. Bunu yaparak sarkacın davranışını doğru bir şekilde tahmin edebiliriz.

Ayrıca büyüleyici olan, ikinci dereceden denklemin farklı çözüm türlerinin diferansiyel denklemin oldukça farklı çözümlerine yol açmasıdır. Eğer $b^2> 4ac$ ise ikinci dereceden denklemin iki gerçek çözümü vardır.

Daha İyi Bir Bisiklet Tasarlama

Her ne kadar bisikletler oldukça basit olsa da bir asırdan fazla bir süre boyunca cevapsız kalmış bazı ilginç sorular içeriyorlar. Örneğin hangi kuvvetler bir bisikletin sabit kalmasını sağlıyor ve neden hareketli binicisiz bir bisiklet kendi kendine dengede kalabiliyor (hızını koruduğu sürece)? Matematikçiler, fizikçiler ve mühendisler, bu tür sorulara cevap vermek ve alıştığımızdan daha kolay dengelenebilen ve yönlendirilebilen yeni tasarımları denemek için diferansiyel denklemler, geometri ve doğrusal cebir içeren modelleri kullanıyorlar.

Mevcut bisiklet tasarımı, titiz analizden ziyade deneme ve yanılmayla gelişti.Araştırmacılar kısa bir süre önce sistemin ana bileşenlerin (tekerlekler, çerçeve ve direksiyon çatalı) tanımlayan denklemleri oluşturmak için matematik ve mekaniği kullandıklarında, stabilite elde etmek için ön tekerlekle yer arasındaki temas noktasının direksiyon ekseninin arkasında olması gerektiği şeklindeki uzun süredir devam eden varsayımla çelişen bir keşif yaptılar. Önce matematik sonra da deneyler, varsayıma uymayan bir bisikletin hala dengede durabileceğini doğruladı.

Gradyanlar

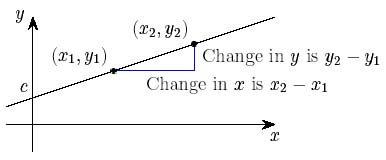
Şekil 1: Doğrunun gradyanı

Basit bir örnekle, yanda şekil 1'de gösterilen doğruyu düşünerek başlayalım. Doğrunun eğimi, $$\frac {\mbox{y'deki değişim}}{\mbox{x'deki değişim}}.                               (1)$$ olarak tanımlanır. Doğru üzerinde iki ayrı nokta $ (x_1, y_1) $ ve $ (x_2, y_2) $ alırsak gradyan aşağıdaki gibi tanımlanır:
$$m: = \frac {y_2-y_1} {x_2-x_1}.$$
Bu, hangi noktaları aldığımıza bağlı değildir. $ m $ 'yi bu şekilde tanımlarken doğrunun denklemi
$$y = mx + c$$ olur. Burada $ c $, doğrunun $ y $ ekseninden geçtiği noktanın $ y $ değeridir.

Fakat Şekil 2'de gösterilen $ x ^ 2 $ fonksiyonunun grafiği gibi düz olmayan eğrilerle ne yapmalıyız? $ x = 3 $ noktasını seçelim ve eğri için $ (3,9) $ noktasında bir gradyana sahip olmanın ne anlama geldiğine karar vermeye çalışalım. Yapacağımız şey bir "teğet" çizmek ve bu doğrunun gradyanını bulmak. Eğrinin gradyanı, bu doğrunun gradyanı olarak tanımlanacaktır. "Verilen noktada $ x ^ 2 $ fonksiyonuyla aynı gradyana sahip" bir doğru bulmaya çalışmakla korkunç bir dolambaçlı iddiaya giriyoruz. Ancak gradyanın ne olduğunu henüz bilmediğimizden problem yok! Bunun yerine, bir teğet çizgisinin ne olabileceği konusunda biraz fikir sahibi olmaya çalışalım.

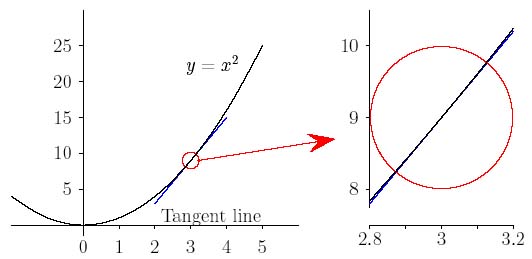Şekil 2: x = 3'de y = x² gradyanını bulma

Diferansiyel denklemler

Asla değişmeyecek olan şey, dünyanın sürekli değiştiği gerçeğidir. Matematiksel olarak, değişim oranları türevlerle tanımlanır. Çevrenizdeki dünyayı tanımlamak için matematik kullanmaya kalkarsanız - bir bitkinin büyümesi, borsa dalgalanmaları, hastalıkların yayılması veya bir nesneye etki eden fiziksel kuvvetler gibi - bir süre sonra kendinizi fonksiyonların türevleriyle uğraşırken bulursunuz. Bunların birbirleriyle ve diğer matematiksel parametrelerle ilişkileri diferansiyel denklemler ile açıklanmaktadır. Bu denklemler, doğal fenomenlere yönelik matematiğin hemen hemen tüm modern uygulamalarının kalbinde yatmaktadır. Uygulamalar neredeyse sınırsızdır ve modern teknolojinin çoğunda hayati bir rol oynamaktadır.

Türev alma: Matematiksel büyüteç.

Bazen, matematik gerçekten tutarlı bütünlükten ziyade prosedür ve tekniklerden oluşan bir koleksiyona benziyor olabilir. Böyle bir kural koleksiyonu, bir fonksiyonla tanımlı bir eğrinin belirli bir noktasında eğim veya "gradyan"ın nasıl bulunacağını bize bildirir. Bu daha çok türev alma olarak bilinir ve analizin bir parçasıdır.

Gradyanlar hakkında biraz bilgi vererek başlıyoruz. Özellikle hangi fonksiyonların iyi tanımlanmış bir gradyana sahip olduğuna ve hangilerinin olmadığına bakacağız. Daha sonra iki fonksiyonun gradyanlarını her noktada hesaplarız: $ x ^ 2 $ ve $ \ sin (x) $. Burada verilmek istenen mesaj cevapları bulmakla ilgili değildir (daha önce analiz konusunu gördüyseniz muhtemelen cevabın sırasıyla $ 2x $ ve $ \ cos (x) $ olduğunu bilirsiniz), fakat limit kavramı bağlamında ilgili yöntemi anlamaktır. Limit konusu, matematikte analiz olarak bilinen bir konuya aittir. Bu, uygulamalı matematiğin pek çok aracını destekleyen merkezi bir işlemdir.