Bazı fonksiyonların grafiklerine büyütme altında bakıldığında düz olmadıkları görülür. Örneğin aşağıdaki şekilde tanımlı |x| fonksiyonu x=0 noktasında düz değildir:
 |
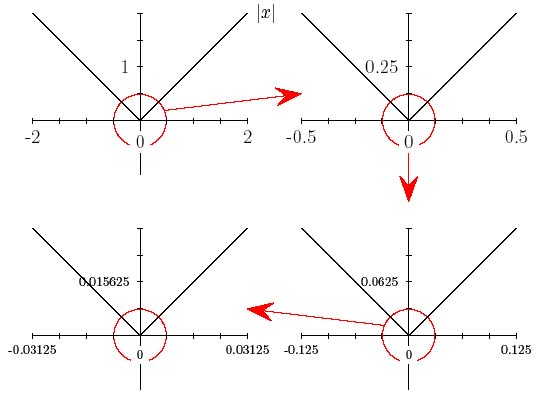
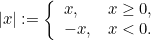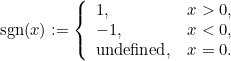| Şekil 4: Farklı büyütmeler altında |x| grafiği |
Farklı büyütmeler altında verilen yukarıdaki grafikler (0,0) noktasında hep "dirsekli" görünecektir. Bu noktada eğriye bir teğet doğrusu yerleştirmek mümkün değildir. Ancak bu nokta dışında grafik
düzdür. 0 haricindeki noktalarda fonksiyonun gradyanı x < 0 için -1 ve x > 0 için 1 dir; diğer bir deyişle x'in işaretidir:
Diğer bir örnek olarak aşağıdaki fonksiyon verilebilir:
 |
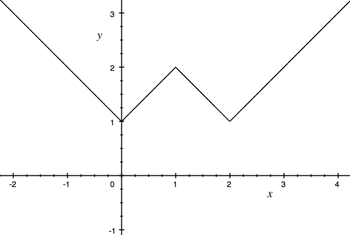| Şekil 5: f(x) = |x| - |x-1| + |x-2| |
|
Aşağıdaki örnekte ise x=2 noktasında bir dirsek bulunmaktadır:
 |
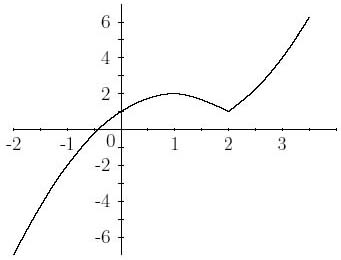| Şekil 6: f(x) = x|x-2| + 1 |
Dahası bu şekilde sonsuz sayıda kötü noktaya sahip fonksiyonlar üretmek mümkündür. Aslında, aşağıda gösterilen grafik her noktada bir "bükülme"ye sahip sürekli bir fonksiyondur! Daha doğrusu, eğrinin herhangi bir noktasında eğimi tanımlayamayız.
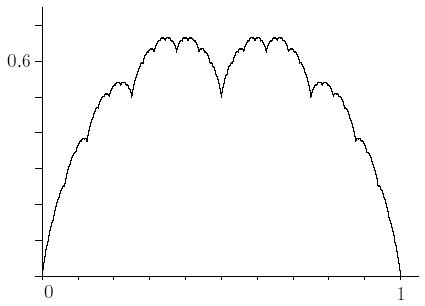
Şekil 7: Hiçbir yerde yüksek büyütme altında düz hale gelmeyen bir fonksiyon
Bunun gibi örnekler, fonksiyon bile olup olmadıklarını tartışan bazı 19. yüzyıl matematikçileri tarafından canavar olarak görülüp göz ardı edildi. Ancak bunlar matematiği şaşırtıcı ve ilginç kılan şeylerdir. Aslında bu tür örnekler çok daha yaygındır, çünkü matematik ders kitabı örneklerine uygulama deneyimi bizi inanmaya yönlendirir. Daha da önemlisi, fraktal olarak bilinen bu tür nesneler, dağlar, sahil şeridi, kırıklar, çatlaklar vb. gibi fiziksel nesnelerin şekillerini tanımlamak için çok yararlıdır. Bu belki de en ünlü örnektir ve sonsuz sayıda testere dişi benzeri fonksiyonun bir araya getirilmesiyle oluşturulmuştur.
