
İkinci dereceden denklemler ile ikinci dereceden diferansiyel denklemler arasındaki bağlantı tesadüf değildir: hepsi Newton'un ikinci yasasında tanımlanan kuvvet ve ivme arasındaki bağlantıyla bağlantılıdır. Newton bu yasayı formüle ettiğinde esas olarak katı cisimlerin hareketini düşünüyordu. Bununla birlikte, su ve hava gibi sıvıların taşınması için de aynı yasaların uygulanabileceği kısa sürede fark edildi. Özellikle, bir sıvının hızı ile basıncı arasındaki ilişkiyi bulmak için Newton yasalarını kullanmak mümkündür. Bu yasaların (Navier-Stokes ve ilgili kısmi diferansiyel denklemler olarak adlandırılır) sofistike versiyonları hava durumunu tahmin etmek için büyük bilgisayarlarda çözülür. Bununla birlikte, birçok sıvı akışı tipi için geçerli olan belirli bir çözüm, uçuşun temel prensiplerinin keşfindeki anahtar bileşenlerden biriydi. Bunun sonuçları ölçülemezdi ve (her zamanki gibi) Bernouilli denklemi olarak adlandırılan ikinci dereceden bir denklemle bağlantılıdır.
Bernoulli ailesi, hem bireysel hem de birlikte matematikte muazzam ilerlemeler kaydeden birçok matematikçiden oluşuyordu. Örneğin Jacob Bernoulli, havanın hareket yolunu inceledi.
Eğer $u$ hızı ve $P$ basıncı ile sürekli hava akışına bakarsanız ve bir hava parçacığı $h$ yüksekliğinde hareket ediyorsa, aşağıdaki denklemi sağlayan bir sabit $E$ (hava parçacığının enerjisi) olduğunu keşfetti:$$u^2/2+P=h.$$
Önemli bir şekilde, eğer $h$ sabitse, bu formül $u$ artarsa $P$'nin azaldığını tahmin eder. Buna Bernouilli etkisi denir. Bu sonuç, Newton'un hareket yasalarının doğrudan bir sonucudur ve sadece çok yapışkan olmayan (viskoz) düzgün hareket eden sıvılar için geçerlidir. Bununla birlikte, bu ikinci dereceden denklem, bir uçağın kanadı üzerindeki hava akışının davranışını tahmin etmek ve bir uçağın nasıl uçtuğunu görmek için yeterince doğrudur.
Bernoulli etkisini gösterebilen bir dizi basit deney vardır. En basitlerinden biri, birkaç santimetre arayla pamuk ipliğine iki pinpon topu asmaktır. Sonra aralarında hafifçe üfleyin ve neler olduğunu izleyin. Ayrılmak yerine birlikte hareket ederler.
Bu, bir sıvının (hava) uyguladığı basıncın, sıvının hızı arttıkça azaldığını gösterir. Hareketli bir sıvının daha fazla baskı yapmasını bekleyebilirsiniz, ancak burada sıvının kendisinin momentumunun ürettiği kuvvetten değil, yanal basınçtan bahsediyoruz. Rüzgar eserken hissettiğiniz kuvvet budur.
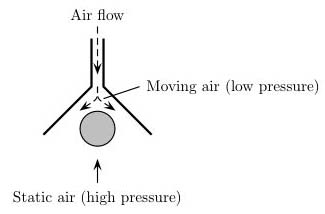
Gerçekten işleyen daha ekstrem bir deney, başka bir pinpon topu içerir. Bu, aşağı doğru hava akışına sahip bir baş aşağı huni içinde durgın halden serbest bırakılır.
Sürekli bir hava akışı ve yeterince büyük bir huni kullanıyorsanız, pinpon topunu dengeleyebilmelisiniz. Pratikte geriye doğru bir elektrikli süpürge, bir pinpon topu ve büyük bir mutfak hunisi gerçekten çok iyi çalışıyor. Bu, havanın aşağı inişi topu emiyor gibi göründüğü için çok garip görünüyor. Ancak, fiziksel prensip ile mükemmel bir uyum içindedir!