İkinci Dereceden Denklemlerin 101 Kullanımı: Kuadratik Kaos - 2

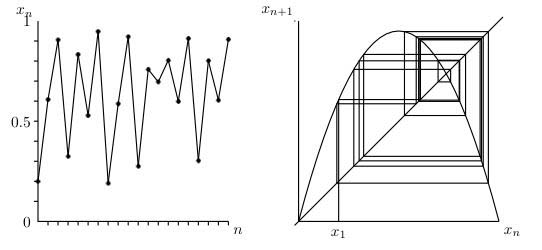
Yukarıdaki şekil $x_1 = 0,2$ ve $r = 3,7$ ile lojistik haritayı göstermektedir. Sistemin çok karmaşık görünen ve öngörülemeyen davranışına dikkat edin. Solda grafiksel bir çizim var. Sağdaki resim örümcek ağları olarak biliniyor çünkü biraz örümcek ağına benziyor. Bu, böcek popülasyonlarının davranışını görselleştirmenize yardımcı olacak grafiksel bir prosedürdür.

İkinci Dereceden Denklemlerin 101 Kullanımı: Kuadratik Kaos

Belirli bir böcek türünün popülasyonunun yıldan yıla nasıl değiştiğiyle ilgilenen bir biyolog veya ekolojist olduğunuzu hayal edin. Bazı böceklerin yılda yalnızca bir jenerasyonu vardır ve basit bir model, gelecek yıldaki nüfusun yalnızca mevcut yıldaki nüfusa bağlı olacağını varsayar. Yani, $x_n$, $n$ yılının popülasyonuysa $x_{n + 1}$, $x_n$'nin bir fonksiyonu olacaktır.

Çok basit bir model bir oranın, yani $ax_n$'nin başarılı bir şekilde ürediğini ve $bx_n^2$'nin aşırı kalabalıktan öldüğünü varsayar. Denklemleri basitleştirmek üzere bir sabit sayı $r> 0$ ve başlangıç ​​popülasyonu $x_1$ için aşağıdaki ikinci dereceden denklemi elde etmek üzere koordinatları yeniden ölçeklendirebiliriz:$$x_{n + 1} = rx_n (1-x_n)$$Kesin olarak söylemek gerekirse $r$ sabitiyle etiketlenen bütün bir ikinci dereceden denklem ailesi tanımladık. Bu ailenin her bir üyesi lojistik harita olarak bilinir.

İkinci Dereceden Denklemlerin 100 Kullanımı: Cep Telefonları

Karmaşık bir ikinci dereceden denklemin cep telefonlarıyla ilgisi nedir? Durup bir an için bir sayının karesini aldığımızda ne olacağını düşünelim: Yani x'i alıp $x^2$'yi hesaplayalım. Fark edeceğimiz şey, x için hangi değeri alırsak alalım $x^2$'nin her zaman negatif olmadığıdır. Sonuç olarak $x^2=-1$'in bir çözümü olamaz. Matematikçilerin bu problemle başa çıkma yolu hilelidir ve varlık açısından bir çözüm tanımlamaktır! $i$ harfi $$x^2=-1$$ dekleminin bir çözümünü temsil etmek için kullanılır, dolayısıyla $i^2=-1$. Yani, $i$ gerçek bir sayı olamaz ve bu nedenle buna sanal sayı denir. $$(-i)^2 = -1 \times i \times -1 \times i = i\times i = -1$$ eşitliğine de dikkat edin. Yani $x = -i$ aynı zamanda $x ^ 2 = -1$ denkleminin bir çözümüdür.

İkinci Dereceden Denklemlerin 100 Kullanımı: Uçuş

İkinci dereceden denklemler ile ikinci dereceden diferansiyel denklemler arasındaki bağlantı tesadüf değildir: hepsi Newton'un ikinci yasasında tanımlanan kuvvet ve ivme arasındaki bağlantıyla bağlantılıdır. Newton bu yasayı formüle ettiğinde esas olarak katı cisimlerin hareketini düşünüyordu. Bununla birlikte, su ve hava gibi sıvıların taşınması için de aynı yasaların uygulanabileceği kısa sürede fark edildi. Özellikle, bir sıvının hızı ile basıncı arasındaki ilişkiyi bulmak için Newton yasalarını kullanmak mümkündür. Bu yasaların (Navier-Stokes ve ilgili kısmi diferansiyel denklemler olarak adlandırılır) sofistike versiyonları hava durumunu tahmin etmek için büyük bilgisayarlarda çözülür. Bununla birlikte, birçok sıvı akışı tipi için geçerli olan belirli bir çözüm, uçuşun temel prensiplerinin keşfindeki anahtar bileşenlerden biriydi. Bunun sonuçları ölçülemezdi ve (her zamanki gibi) Bernouilli denklemi olarak adlandırılan ikinci dereceden bir denklemle bağlantılıdır.

İkinci Dereceden Denklemlerin 100 Kullanımı: Newton - 2

Bir bilgisayar kullanarak böyle denklemlere yaklaşık çözümler bulmak mümkündür ve bu genellikle modern teknolojide karşılaşılan çok karmaşık diferansiyel denklemler için kullanılan yaklaşımdır. Ancak matematikçi Leonhard Euler, ikinci dereceden bir denklemin çözümüne dayanan bu özel denklemi çözmenin bir yolunu tasarladı. Euler, $$x(t)=e^{wt}$$ formunun bir çözümünün varlığını önerdi. Bu fonksiyonun önemi ise şudur: $$\frac{de^{wt}}{dt}=we^{wt}.$$Diferansiyel denkleme yerleştirip $e^{wt}$ ile bölersek $w$ değişkenli aşağıdaki denklemi buluruz:$$aw^2+bw+c=0.$$Bu çok tanıdık! Orijinal diferansiyel denklemi çözmek için tek yapmamız gereken bu ikinci dereceden denklemi çözmek ve $w$ yerine geri koymaktır. Bunu yaparak sarkacın davranışını doğru bir şekilde tahmin edebiliriz.

Ayrıca büyüleyici olan, ikinci dereceden denklemin farklı çözüm türlerinin diferansiyel denklemin oldukça farklı çözümlerine yol açmasıdır. Eğer $b^2> 4ac$ ise ikinci dereceden denklemin iki gerçek çözümü vardır.

İkinci Dereceden Denklemlerin 100 Kullanımı: Newton - 1

Newton, Galileo'nun öldüğü yılda doğdu ve bilimi ve matematiğin bilimsel öngörülebilirlikte oynadığı rolü anlama yolumuzu oluşturmaya devam etti. Newton, hem Galileo'nun hem de Kepler'in çalışmalarından ilham aldı. Bu bilimsel devler, dinamik ve gök mekaniği olaylarını doğru bir şekilde tanımlamışlardı; ancak ikisi de bilimsel açıklamaları formüle etmemişti. Gözlemledikleri fenomenin matematiksel açıklamasını sağlamak Newton'a kalmıştı.

İlk olarak Galileo'nun gözlemlerini açıklayan üç hareket yasasını formüle etti. İkinci olarak iki kütlenin, aralarındaki mesafenin karesiyle ters orantılı bir kuvvetle birbirlerine doğru çekildiği temel kütle çekim yasasını tanımladı. Geometrik argümanları kullanarak böyle bir kuvvet yasasının, gezegenlerin bir konik şeklinde güneşin etrafında hareket etmesi gerektiğine işaret ettiğini kanıtladı. (Elbette, ters kare yasasının bilinen eğrilerle açıklanabilecek yörüngelere yol açması muazzam bir şanstı!) Newton ayrıca optik alanında da çalıştı ve Galileo'nun kullandığı teleskopların (lenslere dayalı olarak) farklı renklerde ışıkların farklı şekillerde kırılmasıyla sorunlara neden olmuştur. Bir aynaya dayanan bir teleskop tasarlayarak bunu aştı. Tüm noktaları odakta toplamak üzere aynanın alabileceği en iyi şekil, daha önce gördüğümüz yansıtıcı teleskopları doğuran parabolden başka bir şey değildi.

İkinci Dereceden Denklemlerin 100 Kullanımı: Galileo - 2

Photo by Matthew T Rader on Unsplash

Çok önemli bir uygulama da belirli bir $u$ hızıyla seyahat eden bir arabanın durma mesafesini bulmaktır. Bir arabanın böyle bir hızla gittiğini ve frene basıldığını düşünün, ne kadar zamanda araba durur? Gazeteciler bile, özellikle de kazadan kaçınmak anlamına geliyorsa bu soruya ilgi duyabilirler. Aslında bir aracı $u$ hızından 0' a kadar yavaşlatmak için $-a$ sabit ivmesi uygulanırsa o zaman $t$'ye göre çözüp yerine koymak $s$ durma mesafesini verir:$$s=\frac{u^2}{2a}.$$Bu sonucun hepimiz için çok önemli olmasının nedeni, hızınızın iki katına çıkmasının, durma mesafenizi dört katına çıkaracağını öngörmesidir. Bu ikinci dereceden ifadede, kentsel alanlarda neden yavaşlamamız gerektiğine dair kesin kanıtlar görüyoruz, çünkü hızdaki küçük bir azalma durma mesafesinde çok daha büyük bir azalmaya yol açıyor. Burada ikinci dereceden denklemin doğru çözülmesi, kelimenin tam anlamıyla sizin veya bir başkasının hayatını kurtarabilir!

İkinci Dereceden Denklemlerin 100 Kullanımı: Galileo

Photo by JR Korpa on Unsplash

İkinci dereceden bir denklemle tanımlanmış elips ile doğa arasındaki uyum, o dönemlerde dikkate değerdi. Sanki doğa söyler gibiydi: "İşte insanların bildiği bir eğri, biraz kullanalım." Bunun neden doğru eğri olduğunu anlamak için Galileo ve ardından Newton'u beklemek gerekti. Cevap belki de ikinci dereceden denklemlerin bu kadar önemli olması için tek önemli nedendir: İkinci dereceden denklemlerle ivme arasındaki bağlantı. Bu bağlantıyı 17. yüzyılın başında ilk tespit eden Galileo oldu.

Çoğu kişi, Pisa Üniversitesi'nde renkli bir Matematik Profesörü olan Galileo'yu duymuştur. Kariyerinin son kısmı, Kopernik'in güneş sistemi görüşünün geçerliliği üzerine İspanyol Engizisyonuyla yaptığı destansı savaşa sahne oldu. Bununla birlikte bundan önce yaşamının çoğunu nesnelerin nasıl hareket ettiğini incelemeye adadı. Galileo'dan çok önce Yunan bilim adamı Aristoteles (Aristo), maddenin doğal halinin hareketsiz kalmak olduğunu belirtmişti. Aristoteles ayrıca ağır nesnelerin hafif olanlardan daha hızlı düştüğünü söylemiştir. Galileo bu kabul görmüş bilge sözlerin her ikisine de meydan okudu. Galileo'nun çalışmalarının temelinde, arabamızı ne zaman ve nasıl durduracağımızı ve gol vuruşunun nasıl yapılacağını bilmek gibi hayati faaliyetlerle büyük ölçüde ilişkili olan dinamikleri anlama vardı.

İkinci Dereceden Denklemlerin 100 Kullanımı: Konikler

Yunanlılar ayrıca koni şekliyle de çok ilgilenmişlerdir. Soldaki renkli resim tipik bir koniyi gösterir. Koninin yarısı bir fenerden gelen ışığın yayılması olarak görselleştirilebilir. Şimdi bir meşaleyi duvar gibi düz bir yüzeye tutarsanız, meşaleyi hareket ettirirken çeşitli şekiller göreceksiniz. Bu şekillere konik kesitler denir ve bir düzlemle bir koniyi çeşitli açılardan bölerseniz elde edeceğiniz eğrilerdir. Kesin olarak bu eğriler Yunanlılar tarafından incelenmiştir ve temel olarak dört tür konik kesit olduğunu kabul etmişlerdir. Koninin içinden yatay bir kesit alırsanız o zaman bir çember elde edersiniz. Yatayla küçük açılı bir kesit size bir elips verir. Dikey bir kesit alırsanız hiperbol olur ve koninin bir kenarına paralel bir kesit alırsanız parabol elde edersiniz. Bu eğriler yanda gösterilmektedir.

İkinci Dereceden Denklemlerin 100 Kullanımı: Altın Oran

Bir dikdörtgeni alıp ardından dikdörtgenin kısa kenarı ile aynı kenar uzunluğundaki bir kareyi dikdörtgenden çıkaralım. Dikdörtgenin uzun kenarı 1 uzunluğa ve kısa kenarı $x$ uzunluğa sahipse kare $x$ uzunluğundaki kenarlara sahiptir. Kalan dikdörtgenin uzun kenarı $x$ ve kısa kenarı $1-x$ olur. Şimdiye kadar çok soyut. Ancak Yunanlılar, en estetik oranlara sahip olan (Altın Dikdörtgen adı verilen) dikdörtgenin bu olduğuna inanıyorlardı, çünkü büyük ve küçük dikdörtgenlerin aynı kenar uzunluğu oranlarına sahipti. Bunun mümkün olması için şu gerekir:$$\frac{x}{1} =\frac{1-x}{x} \, \textrm{veya} \, x^2+x=1.$$Bu ise başka bir ikinci dereceden denklemdir: Çok sayıda uygulamada geçen önemli bir denklem. (Pozitif) çözümü şudur:$$x=\frac{\sqrt{5}-1}{2}=0.61803....$$Burada $x$ sayısına altın oran adı verilir ve $\phi$ ile gösterilir.

İkinci Dereceden Denklemlerin 100 Kullanımı: Avrupa'da Kağıt Boyları

Anlaşılmaz bir sayı olmasına karşın $\sqrt{2}$ ile çok sık karşılaşırız: A4 kağıt kullandığımız her an. Avrupa'da kağıt boyları A ölçüleriyle belirtilir, en büyük olan A0 boyutlu kağıt 1 metre karedir. A ölçüleri arasında bir ilişki vardır. Bir A1 kağıdını tam ortadan ikiye katlarsak A2 kağıdını, A2 kağıdını ikiye katlarsak A3 kağıdını ve benzer yolla A4 ve A5 ölçülü kağıtları elde ederiz. Ancak bu kağıtlar her zaman aynı orantıda olacak şekilde düzenlenmiştir.

Peki hangi oranda diye sorabiliriz: Kenar uzunlukları x ve y (x > y) olacak şekilde bir kağıt alalım. Şimdi bunu kenar uzunlukları y ve x/2 olacak şekilde ikiye bölelim (y > x/2). Birinci kağıtta kenarlar oranı x/y iken ikinci kağıtta y/(x/2)=2y/x olur. Bu oranların eşit olmasını istiyoruz. Yani $$x/y=2y/x$$ ya da $$(x/y)^2=2.$$

İkinci Dereceden Denklemlerin 100 Kullanımı: Yunanlar

Şimdi 1000 yıl geriye antik Yunana doğru gidiyoruz ve ikinci dereceden denklemlerden nasıl faydalandıklarını görüyoruz. Yunanlar süper matematikçilerdi ve bugün hala kullandığımız matematiği büyük oranda keşfetmişlerdi. Çözmeye çalıştıkları denklemlerden biri basit bir ikinci dereceden denklemdi: $x^2=1.$

Bu denklemin bir çözümü olduğunu biliyorlardı. Aslında bu, bir birim kenarlara sahip bir dik üçgenin hipotenüs uzunluğuydu.

Pisagor denkleminde kısa kenar uzunlukları 1 alınırsa hipotenüs uzunluğu c=x=$\sqrt{2}$ olarak bulunur.

Bu durumda x nedir, ya da Yunanların sordukları şekliyle, x ne tür bir sayıdır? Bunun sebebi Yunanların oran anlayışından kaynaklanmaktadır. Onların inanışına göre her sayı birbiriyle orantılıdır. Daha kesin bir ifadeyle a ve b tam sayı olmak üzere her sayı a/b şeklinde bir kesirdir. Dolayısıyla $\sqrt{2}$ de bir kesir olmalıdır. Ama olmadığını anlamak büyük bir şaşkınlıktı. Gerçekte $\sqrt{2}$ sayısının ondalık açılımında virgülden sonraki basamaklar sonsuza kadar düzensiz olarak sürmekteydi.

İkinci Dereceden Denklemlerin 100 Kullanımı: Babilliler - 2

Tabii tüm tarlalar kare değildir. Şimdi, çiftçinin sağda gösterildiği gibi iki üçgen kesitli daha garip şekilli bir tarlaya sahip olduğunu varsayalım. Uygun a ve b değerleri için çiftçinin bu alanda büyütebileceği ürün miktarı $$c=ax^2+bx$$ile verilir.

İkinci Dereceden Denklemlerin 100 Kullanımı: Babilliler

9 ile çarpım tablosunu içeren Babil çivi yazısı tabletleri

Her şey Babil'liler ile MÖ 3000 civarında başladı. Onlar dünyanın ilk medeniyetlerinden biriydi ve tarım, sulama ve yazı gibi bazı büyük fikirlerle ortaya çıktılar. Güneş'in, Ay'ın ve gezegenlerin yollarını çizdiler ve bunları kil tabletlerine kaydettiler (Britanya Müzesinde hala görebilirsiniz). Çemberin 360 derece olarak bölünme biçimi de dahil olmak üzere, modern açı fikirlerini Babillilere borçluyuz. Aynı zamanda (korkulan) vergi uzmanının daha az hoş bir icadı için borçluyuz. Ve bu, Babillerin ikinci dereceden denklemleri çözmek için ihtiyaç duydukları nedenlerden biriydi.