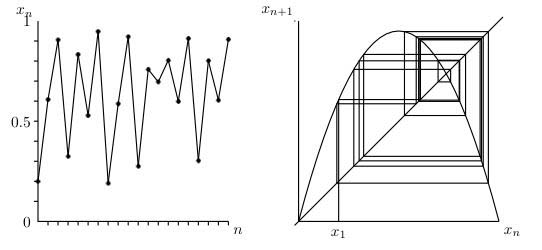
Bir örümcek ağı grafiği çizmek için yapılacak ilk şey r'nin değerini seçmek ve ardından örümcek ağı diyagramında kuadratiği çizmektir. Sonra ilk popülasyon, x eksenindeki $x_1$ ve ayrıca $y = x$ doğrusu. $x_2$'nin değeri, tanım gereği $rx_1 (1-x_1)$'dir, bu sadece grafikteki $x_1$'in değeridir. Bu nedenle, grafiğe çarpana kadar $x_1$'den dikey bir çizgi çizin. Sonra $x_2$'den $y = x$ doğrusuna yatay bir çizgi çizin. Şimdi x ekseni üzerinde $x_2$'nin konumuna sahibiz ve işlemi tekrarlayabiliriz. $x3$'ü bulmak için grafiğe başka bir dikey çizgi ve ardından $y = x$ doğrusuna yatay bir çizgi çizebiliriz. Bu grafik prosedür, sayı listeleri tarafından körleştirilmeden tekrarlanabilir. Bir örümcek ağı diyagramı ile neler olup bittiğine dair mükemmel bir fikir edinebilirsiniz.
Etkileşimli bir applet, kuadratiğin maksimumunu yukarı ve aşağı çekerek farklı r değerleri ile deney yapmanıza izin verecektir. Lojistik haritada maksimum değer $r / 4$ olur ve bu nedenle uygulama, r'yi 0 ile 4 arasında kullanmanıza izin verir. Yatay çubuğu fareyle çekerek de başlangıç popülasyonunu değiştirebilirsiniz.
Bu ikinci dereceden lojistik haritalar, uygulamalı matematiğin modern ve heyecan verici bir alanı olan kaosu göstermektedir. Kaos, sistemin kendisi rastgele olmasa bile görünüşte rastgele davranan bir sistemi tanımlamak üzere kullanılır. En şaşırtıcı olan şey ise çok basit sistemlerin çok karmaşık şekillerde davranmasıdır.
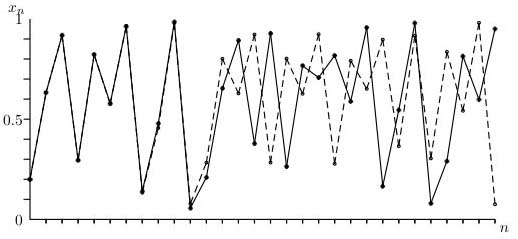
Örneğin aşağıda birbirine çok yakın iki ilk popülasyonu aldığınızda ne olduğunu gösteriyoruz. Özellikle sistemi $x_1 = 0,2$ ardından $x_1 = 0,2001$ ile başlatıyoruz ki bunlar gerçekten çok yakın. Sadece birkaç jenerasyon sonra popülasyonlar tamamen farklı şeyler yapıyor! Nüfusları tahmin etmek isteyip de ilk nüfusları tahmin etmek zorunda kalırsanız bu tür bir davranış felaket olur.
Aslında kaos çok daha fazlasını söylüyor. Gerçekten, ilk böcek popülasyonlarını tahmin ederken herhangi bir hata yaparsanız o zaman çok yakında tahmininiz umutsuzca yanlış olacaktır. Bunun nasıl çalıştığına dair bir fikir edinmek için bir bilgisayar ve $r = 4$ ile lojistik haritayı kullanarak kendiniz bazı deneyler denemelisiniz. Keşfedeceğiniz üzere r'nin tüm değerleri kaos üretmeyecektir. Bilim adamları ve matematikçiler imkansız olabilecek böcek popülasyonunu tahmin etmeye çalışmak yerine, belirli bir sistemin ne zaman kaotik olduğunu anlamaya çalışır. Bunu bilmek, bir tahminin ne zaman doğru ve ne zaman umutsuz olduğunu bilmemizi sağlar. Daha fazla kaos örneği için, Plus'ın 26. sayısından Chris Budd'ın kaos içinde düzeni bulma konusuna bakınız.