İkinci Dereceden Denklemlerin 101 Kullanımı: Kuadratik Kaos - 2

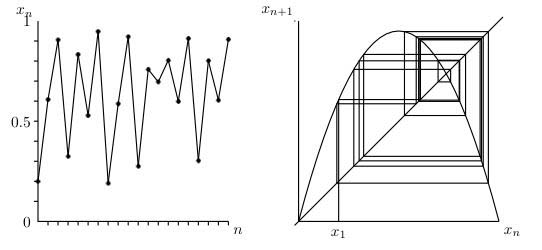
Yukarıdaki şekil $x_1 = 0,2$ ve $r = 3,7$ ile lojistik haritayı göstermektedir. Sistemin çok karmaşık görünen ve öngörülemeyen davranışına dikkat edin. Solda grafiksel bir çizim var. Sağdaki resim örümcek ağları olarak biliniyor çünkü biraz örümcek ağına benziyor. Bu, böcek popülasyonlarının davranışını görselleştirmenize yardımcı olacak grafiksel bir prosedürdür.

İkinci Dereceden Denklemlerin 101 Kullanımı: Kuadratik Kaos

Belirli bir böcek türünün popülasyonunun yıldan yıla nasıl değiştiğiyle ilgilenen bir biyolog veya ekolojist olduğunuzu hayal edin. Bazı böceklerin yılda yalnızca bir jenerasyonu vardır ve basit bir model, gelecek yıldaki nüfusun yalnızca mevcut yıldaki nüfusa bağlı olacağını varsayar. Yani, $x_n$, $n$ yılının popülasyonuysa $x_{n + 1}$, $x_n$'nin bir fonksiyonu olacaktır.

Çok basit bir model bir oranın, yani $ax_n$'nin başarılı bir şekilde ürediğini ve $bx_n^2$'nin aşırı kalabalıktan öldüğünü varsayar. Denklemleri basitleştirmek üzere bir sabit sayı $r> 0$ ve başlangıç ​​popülasyonu $x_1$ için aşağıdaki ikinci dereceden denklemi elde etmek üzere koordinatları yeniden ölçeklendirebiliriz:$$x_{n + 1} = rx_n (1-x_n)$$Kesin olarak söylemek gerekirse $r$ sabitiyle etiketlenen bütün bir ikinci dereceden denklem ailesi tanımladık. Bu ailenin her bir üyesi lojistik harita olarak bilinir.

Fraktalların Penceresinden Dünya'ya Bakmak

Fraktallar, bilgisayar grafiklerini ve simülasyonlarını daha gerçekçi kılan özbenzer (kendilerine benzeyen) matematiksel nesnelerdir. Fraktalların özbenzerliği, bir eğreltiye ya da bir sahile benzer: Her biri orijinaline benzeyen, birbirini izleyen büyütmelerle üretilen görüntüler.

Basit süreçlerden ibaret yinelemeleri içerdikleri için fraktallar genellikle kaos çalışmasında ortaya çıkar. Bir fraktal gibi, kaotik bir sistemin gizli bir karmaşıklığı vardır. Kendisini geri besleyen bir sürecin başlangıcındaki küçük değişiklikler, daha sonra dramatik değişiklikler üretebilir. Bir örnek olarak kelebek etkisi, yani bir kelebeğin kanatlarını çırpmasının birkaç hafta sonra küresel hava koşullarında yapabileceği etki verilebilir.

Kaos Nedir?

T gibi bir dönüşümün kaotik olması için dönüşüm tekrar ve tekrar uygulandığında x değerlerindeki küçük farkları büyütmesi gerekir. Bu ise $dT/dx$ türevinin büyüklüğünün her noktada 1'den büyük olmasını gerektirir.

$dT/dx=-1/x^2, 0<x<1$ olduğundan bu açıktır. Ancak bu büyütme duyarlılığı açıkça üretilen x değerine bağlıdır - değer x=0'a ne kadar yakınsa $|dT/dx|$ o kadar büyüktür. Küçük bir $\delta x$ belirsizliği dönüşümün sayesinde $|dT/dx| \delta x$ değerine büyütülür. Kaotik duyarlılık, büyümenin üstel hızda ($exp{\lambda \delta x}$ gibi) olması anlamına gelir.

$\lambda = \ln |dT/dx|$ duyarlılık kuvvetinin ortalama değerini, T dönüşümü ile bulunan x çıktı değerlerini yöneten Gauss olasılık dağılımı yardımıyla bulacağız. Bu ortalama duyarlılık, h, bazen dönüşümün Kolmogorov veya metrik entropisi olarak adlandırılır ve bu nedenle aşağıdaki gibi verilir: $$h=\int^1_0{ln|dT/dx|}p(x)dx.$$
Önceki yazıda verilen T dönüşümü için değeri şu şekildedir: $$h=\int^1_0{\frac{-2ln(x)}{(1+x)ln2}dx}=\frac{\pi ^2}{6(ln2)}.$$

Kaotik Sayılar

Hemen hemen her gerçel sayıdan sonsuz sürekli kesir açılımı (ska) bölümleri üretme işlemi kaotik bir süreçtir. Genişletmek istediğimiz sayı u₁ olsun ve tam sayı kısmı k, kesir kısmı x₁ olmak üzere
$$u_1=k+x_1$$
şeklinde ayırırız.
Bazen tam kısmını almak üzere k=[u] yazarız, mesela [$\pi$]=3, [e]=2. Şimdi, $\pi$ gibi bir sayı ile başlarsak, ilk k₁ bölümü sadece [$\pi$]=3 olur ve kesir kısmı da x₁=0,141592. Sonraki bölüm
$$k_2=[1/x_1]=[1/0,141592...]=[7,0625459...]=7$$
kesir kısmının tam sayı kısmı olur; sonraki kesir kısmı $x_2=0,0625459...$ ve böylece
$$k_3=[1/x_2]=[1/0,0625459...]=[15,988488...]=15$$
olur. Bu basit süreç daha önce verdiğimiz $\pi$'nin ilk birkaç bölümünü verir. Kesir kısımlar her zaman 0 ile 1 arasında gerçel sayılardır. 0 ve 1'e eşit olamazlar, aksi halde ya u₁ sayısı bir rasyonel kesir olur ya da ska sonlu olurdu. Ardışık kesir kısımları üretme süreci aşağıdaki doğrusal olmayan fark denklemi ile verilir:
$$x_{n+1}=T(x_n)=1/x_n-[1/x_n].$$

Levy Sabiti

Paul Lévy, hemen hemen her sürekli kesir genişlemesine dikkat ettiğimizde, rasyonel yakınsaklar hakkında eşit derecede şaşırtıcı ve genel bir şey söyleyebileceğimizi göstermiştir. Gerçel sayılara rasyonel yaklaşımların$\ n$ arttıkça $q_n^{-2}$ ifadesinin sabit bir katı şeklinde arttığını zaten 21-24 denklemlerinde görmüştük. Hemen hemen her sayı için$\ n$ arttıkça karşılık gelen $q_n$ değerinin üstel olarak o kadar hızlı bir şekilde artamayacağı gösterilebilir (Bir A pozitif sayısı için,$\ n\rightarrow \infty $ iken $\ q_n <e^{An}$). Lévy, temel bir sabit ile belirlenecek gerçek büyüme oranını ayırdı, böylece hemen hemen her gerçel sayının $$\ n \rightarrow \infty, \; q_n^{1/n} \rightarrow L $$ sürekli kesir açılımındaki bölümlerin paydaları için, L Levy sabiti olmak üzere, $$\ L=\exp \{\frac{\pi^2}{12 \ln{2}} \}=3.2758229187 \ldots$$ olduğu bulunur.