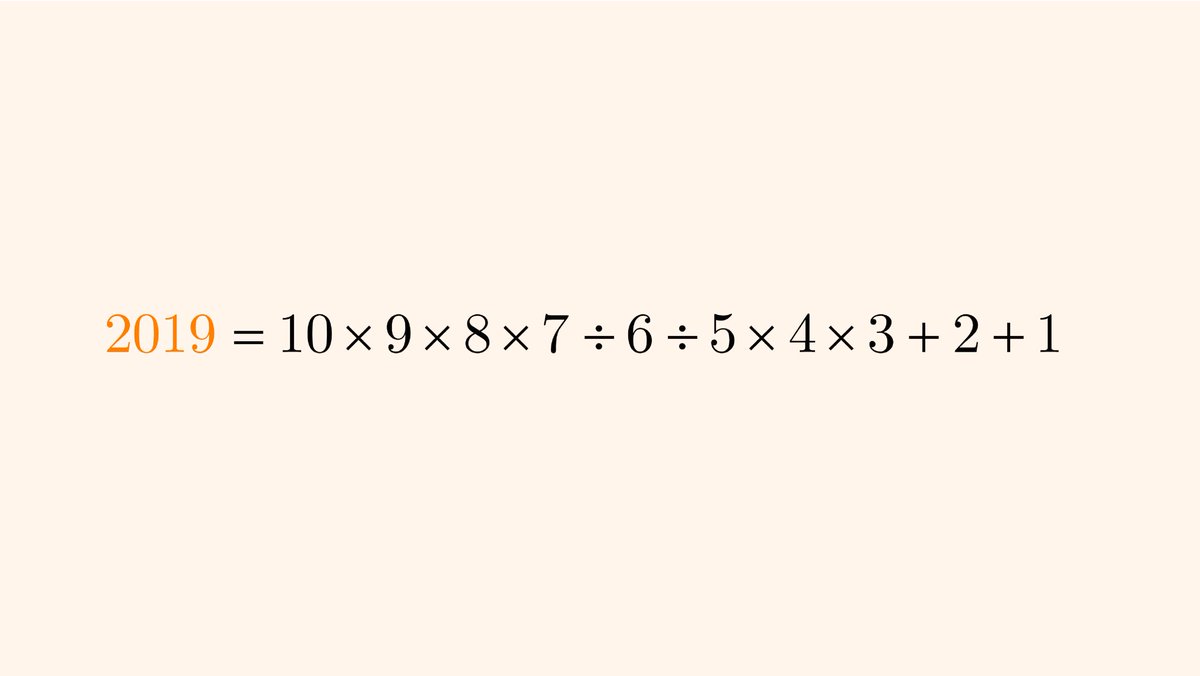2019 ve Matematik

@MathsEdIdeas

Şaşırtıcı Sayı Modelleri 2

Sayı sisteminin şaşırtıcı doğasına dayanan, matematiğin cezbedici taraflarına örnekler vermeye devam ediyoruz. Güzelliği açıklamaya gerek yok, ilk görüşte anlaşılıyor zaten. Sadece bakın, zevkine varın ve paylaşın. Ve aynı şekilde bunların değerini anlamaya çalışıp, mümkünse bir açıklama vermeye çalışın.

12345679*9=111,111,111

12345679*18=222,222,222

12345679*27=333,333,333

12345679*36=444,444,444

12345679*45=555,555,555

12345679*54=666,666,666

12345679*63=777,777,777

12345679*72=888,888,888

12345679*81=999,999,999

Sayılardaki Güzellik

Steve Spangler Science

Şaşırtıcı Sayı Modelleri 1

Matematiğin cazibesinin, şaşırtıcı sayı sisteminden kaynaklandığı zamanlar olur. Bu cazibeyi göstermek için fazla söze gerek olmaz. Elde edilen desenlerde bu açıkca görünür. Bakın, zevk alın ve bu hayret verici özellikleri diğerlerine yayın. Onların da bunların farkında olmalarını sağlayın ve eğer mümkünse, bunun bir açıklamasını bulmaya çalışın. Daha önemlisi öğrencilerin bu sayı desenlerindeki güzellikleri anlayabilmeleridir.

1*1=1
11*11=121
111*111=12,321
1111*1111=1,234,321
11111*11111=123,454,321
111111*111111=12,345,654,321
1111111*1111111=1,234,567,654,321
11111111*11111111=123,456,787,654,321
111111111*111111111=12,345,678,987,654,321

Twitter Math: Jim Wilder

Twitter'da matematikle ilgili çok ilginç sayfalar bulabilirsiniz. İşte biri:
$$225 = 1^3+2^3+3^3+4^3+5^3 \\ 225 = (1+2+3+4+5)^2 \\ 216^2 - 513^2 = -216513 \\ 209 = 1^6+2^5+3^4+4^3+5^2+6^1 \\ 3435 = 3^3+4^4+3^3+5^5 \\ 1306 = 1^1+3^2+0^3+6^4 \\ 1676 = 1^1+6^2+7^3+6^4$$

Quanta Magazine: Sezgi Problemleri

https://www.quantamagazine.org/

Quanta Magazine, Simon organizasyonu tarafından kurulmuş, halkın bilimi anlamasını sağlama ve geliştirmeyi amaçlayan çevrimiçi bir dergidir.

Matematik, fizik, biyoloji ve bilgisayar bilimlerinde yazılan yazılarda bilimin karmaşıklığı yumuşak bir anlatımla ele alınıyor. Gelecek yazılarımızda buradan yapacağımız çevirilerle bu siteyi tanıtmaya ve edindiği amacı ulaştırmaya çalışacağız. Özellikle bulmaca ve ilginç soruları ele alacağız.

İlk olarak sonlu ile sonsuz arasında köprü olmaya çalışan, sonlu sayıları sonsuzlukla ifade etmeye çalışan bir matematikçi olan Ramanujan'dan ilginç bir soru:

$$\sqrt{1+2\sqrt{1+3\sqrt{1+4\sqrt{1+5\sqrt{...}}}}}=?$$