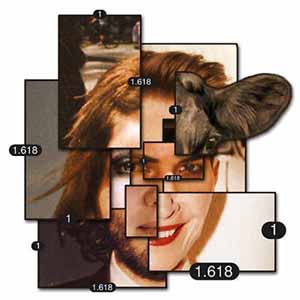
"Ya susmak ya da suskunluktan daha kıymetli bir söz söylemek gerekir." Pisagor
altın oran etiketine sahip kayıtlar gösteriliyor. Tüm kayıtları göster
altın oran etiketine sahip kayıtlar gösteriliyor. Tüm kayıtları göster
24 Ağustos 2019
İkinci Dereceden Denklemlerin 100 Kullanımı: Altın Oran

Labels:
altın oran,
denklem,
fibonacci,
ikinci dereceden,
plus magazine
19 Mayıs 2017
Herkesin Güzellik Anlayışı Farklı Mıdır?
Bu alandaki öncü (oldukça ilkel) deneyler 1860'larda Alman fizikçi ve psikolog Gustav Theodor Fechner tarafından yapıldı. Fechner'in deneyi basitti: en-boy oranları farklı on dikdörtgen bir deneğin önüne konularak en hoşuna gideni seçmesi isteniyor. Seçimlerin %76'sı 1,75, 1,62 ve 1,50 oranlarına sahip üç dikdörtgenden oluşuyor (ki "Altın Dikdörtgen" için bu oran 1,62). Fechner daha ileri giderek dikdörtgen şekilli binlerce nesnenin (pencereler, çerçeveler, kitaplar) boyutlarını ölçtü ve ( Vorschule der Aesthetik adlı eserinde) yaklaşık oranı Altın Orana yakın bulduğunu iddia etti. Birçok psikolog daha sonra benzer deneyler yaptılar ve oldukça tutarsız sonuçlar elde ettiler. Örneğin Toronto Üniversitesi'nden Michael Godkewitsch çoğu zaman ortalama grup tercihlerinin en çok tercih edilen seçimleri yansıtmadına işaret etti. Mesela herkesin en iyi ikinci olarak değerlendirdikleri bir çay markası ortalamada en iyi olarak görülebilir, fakat belki de hiç kimse bunu satın almayacak. Godkewitsch bu nedenle ilk tercihlerin ortalamalardan daha anlamlı bir tercih ölçüsü olarak alınabileceğini ifade etti. 1974'te yaptığı bir çalışmasında, daha önceki deneylerde rapor edilen Altın Oran tercihinin deneklere sunulan dikdörtgenler kümesinde dikdörtgenin konumunun bir yapay olgu olabileceği sonucuna vardı. Bununla birlikte diğer deneylerde farklı sonuçlar elde edildi.
Labels:
altın dikdörtgen,
altın oran,
estetik,
fibonacci,
plus magazine,
sanat
12 Mayıs 2017
Altın Oran ve Estetik
Kutsal oranın kökenleri
Elementler kitabında, yazılan en etkili matematik ders kitabı, Öklid adına "uç ya da ortalama oran" dediği bir doğrunun bölümlerinden elde edilen bir oran tanımlar. Tanım şöyledir:
"Bir doğru, kendisinin büyük parçaya oranı, büyük parçanın küçük parçaya oranına eşit olacak biçimde bölündüğünde, uç ya da ortalama oranda bölünmüştür denir."
Diğer bir ifadeyle, aşağıdaki şekilde, C noktası doğruyu öylesine böler ki AC/CB oranı AB/AC oranına eşittir. Bazı temel cebir kitapları bu durumda AC/CB oranının $1/\sqrt{5}=1,618..$ irrasyonel sayısına eşit olduğunu gösterirler.
Kim tahmin edebilir di ki bu masum görünüşlü bölümleme bitkilerin yaprak ve tohum düzenlerinden bazı aluminyum alaşımlarının kristal yapılarına, borsadan sanata değişen sayısız doğal bilinmezlere burnunu soksun?
Gerçekten Öklid'in tanımından sonra geçen yüzyıllar içinde bu sayının şaşırtıcı birçok özelliğinin ortaya çıkmasıyla bu sayıya "Kutsal oran " ya da "Altın oran" onursal isimleri verildi.
Bu yazıda yazar Mario Livio, Altın oranın sadece estetik özellikleri ve bunun matematikle olan ilişkisi üzerinde duruyor.
Elementler kitabında, yazılan en etkili matematik ders kitabı, Öklid adına "uç ya da ortalama oran" dediği bir doğrunun bölümlerinden elde edilen bir oran tanımlar. Tanım şöyledir:
"Bir doğru, kendisinin büyük parçaya oranı, büyük parçanın küçük parçaya oranına eşit olacak biçimde bölündüğünde, uç ya da ortalama oranda bölünmüştür denir."
Diğer bir ifadeyle, aşağıdaki şekilde, C noktası doğruyu öylesine böler ki AC/CB oranı AB/AC oranına eşittir. Bazı temel cebir kitapları bu durumda AC/CB oranının $1/\sqrt{5}=1,618..$ irrasyonel sayısına eşit olduğunu gösterirler.
Kim tahmin edebilir di ki bu masum görünüşlü bölümleme bitkilerin yaprak ve tohum düzenlerinden bazı aluminyum alaşımlarının kristal yapılarına, borsadan sanata değişen sayısız doğal bilinmezlere burnunu soksun?
Gerçekten Öklid'in tanımından sonra geçen yüzyıllar içinde bu sayının şaşırtıcı birçok özelliğinin ortaya çıkmasıyla bu sayıya "Kutsal oran " ya da "Altın oran" onursal isimleri verildi.
Bu yazıda yazar Mario Livio, Altın oranın sadece estetik özellikleri ve bunun matematikle olan ilişkisi üzerinde duruyor.
Labels:
altın oran,
fibonacci,
köken,
kutsal oran,
plus magazine,
tarihi
2 Mayıs 2017
Fibonacci: Altın Büyüme
Botanikçiler bitkilerin, meristem adı verilen büyüyen bitkinin tepesinde bulunan bir grup hücreden büyüdüklerini gösterdiler. Her dalda büyümeyi devam ettiren meristem dokular mevcuttur. Bir kere oluştumu bitki boyut olarak büyür ama yeni hücreler sadece bu büyüme noktalarında oluşur. Gövdenin altında kalan hücreler genişledikçe meristem yükselir. Bu hücreler aynı zamanda spiral yaparak büyürler: meristem sanki dönüyormuş gibi görünür, yeni bir hücre oluşur, meristem belli bir açıyla diğer yeni hücreleri oluşturur ve böylece devam eder. Bu hücreler daha sonra tohum, yaprak, dal veya çiçek üzerinde taç yaprak ve ercik halini alırlar.
Şekilde yapraklar oluşma sırasına göre numaralandırılmıştır. Her biri öncekine göre saat yönünde bir tam dönüşün 0,618 katı dönüşle (222,5 derece) yerleşmiştir.
İlginç olan şu ki bitki ne kadar büyürse büyüsün tek bir sabit dönme açısı optimal deseni oluşturabilir. Tek bir açı dönüşünün tekdüze dizilim üretmesi prensibi yüzyılın başına kadar şüpheyle karşılanıyordu fakat 1993'de iki Fransız matematikçi, Stephane Douady ve Yves Couder, matematiksel olarak ispatladılar. Evet tam bir dönüşün 0,618 katı dönüşle yeni hücre oluşumu optimal dizilimi gerçekleştirmektedir, ama nereden geliyor bu 0,618 sayısı?
Şekilde yapraklar oluşma sırasına göre numaralandırılmıştır. Her biri öncekine göre saat yönünde bir tam dönüşün 0,618 katı dönüşle (222,5 derece) yerleşmiştir.
İlginç olan şu ki bitki ne kadar büyürse büyüsün tek bir sabit dönme açısı optimal deseni oluşturabilir. Tek bir açı dönüşünün tekdüze dizilim üretmesi prensibi yüzyılın başına kadar şüpheyle karşılanıyordu fakat 1993'de iki Fransız matematikçi, Stephane Douady ve Yves Couder, matematiksel olarak ispatladılar. Evet tam bir dönüşün 0,618 katı dönüşle yeni hücre oluşumu optimal dizilimi gerçekleştirmektedir, ama nereden geliyor bu 0,618 sayısı?
Labels:
altın oran,
fi sayısı,
fibonacci,
plus magazine
25 Nisan 2017
Fibonacci: Spiraller ve Kabuklar
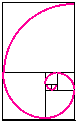
 Arı populasyonları Fibonacci sayılarının ortaya çıktığı doğadaki tek alan değildir. Kabukların güzel şekillerinde de görünürler. Bunu göstermek için iki tane bitişik birim kare alalım. Bunlara komşu hemen üzerine 2 (=1+1) birimlik bir kare çizelim. Ardından bu yeni kareye ve önceki birim kareye komşu 3 (=1+2) birim kenarlı yeni bir kare çizelim. Ve yine birim karelere ve 3 birimlik kareye komşu 5 (=2+3) birim kenarlı yeni bir kare çizelim. Bu şekilde peşpeşe önce çizilen iki kareye komşu olacak şekilde ve kenar uzunluğu önceki iki karenin kenar uzunlukları toplamına eşit olan kareler çizebiliriz. Kenar uzunlukları iki ardışık Fibonacci sayısı olan ve kenar uzunlukları Fibonacci sayıları olan karelerden oluşan bu dikdörtgenlere Fibonacci Dikdörtgenleri adı verilir.
Arı populasyonları Fibonacci sayılarının ortaya çıktığı doğadaki tek alan değildir. Kabukların güzel şekillerinde de görünürler. Bunu göstermek için iki tane bitişik birim kare alalım. Bunlara komşu hemen üzerine 2 (=1+1) birimlik bir kare çizelim. Ardından bu yeni kareye ve önceki birim kareye komşu 3 (=1+2) birim kenarlı yeni bir kare çizelim. Ve yine birim karelere ve 3 birimlik kareye komşu 5 (=2+3) birim kenarlı yeni bir kare çizelim. Bu şekilde peşpeşe önce çizilen iki kareye komşu olacak şekilde ve kenar uzunluğu önceki iki karenin kenar uzunlukları toplamına eşit olan kareler çizebiliriz. Kenar uzunlukları iki ardışık Fibonacci sayısı olan ve kenar uzunlukları Fibonacci sayıları olan karelerden oluşan bu dikdörtgenlere Fibonacci Dikdörtgenleri adı verilir.Şimdi her karenin içine uç uca gelecek şekilde çeyrek çemberler çizecek olursak bir tür spiral eğrisi elde ederiz. Bu gerçek bir matematiksel spiral eğrisi değildir (çünkü sadece çember parçalarından oluşuyor ve gittikçe küçülen formda değil) ama doğada görünen bir çeşit spiral eğrisine iyi bir yaklaşımdır. Böylesi spiral eğrileri salyangoz kabukları ve deniz kabukları şekillerinde görülür. Aşağıda bir deniz helezonunun ara kesiti gösterilen resimde kabuğun spiral eğrisi gösteriliyor ve hayvanın kullandığı iç hazneler hayvan büyüdükçe ekleniyor. Hazneler suda kaldırma kuvveti sağlıyor.
Labels:
altın oran,
doğa,
fibonacci,
kabuk,
plus magazine,
spiral
17 Nisan 2017
Fibonacci: Arılar Daha İyi
Tavşan problemi açıkça çok zoraki görünüyor, fakat Fibonacci dizisi gerçek populasyonlarda oluşmaktadır. Bal arıları buna bir örnek. Bir bal arısı kolonisinde kraliçe denen özel bir dişi bulunur. Diğer dişiler kraliçenin aksine yumurta üretmeyen işçi arılardır. Erkek arılar ise çalışmazlar.
Erkek arılar kraliçenin döllenmemiş yumurtalarından çıkarlar, yani erkek arıların anneleri var fakat babaları yoktur. Dişi arılar ise döllenmiş yumurtadan çıkarlar ve hem anne hem de babaları bulunur. Dişiler genelde işçi olurlar ama bazıları arı sütü ile beslenerek kraliçe olurlar ve yeni bir koloni kurmak üzere kovandan ayrılırlar.
Erkek arılar kraliçenin döllenmemiş yumurtalarından çıkarlar, yani erkek arıların anneleri var fakat babaları yoktur. Dişi arılar ise döllenmiş yumurtadan çıkarlar ve hem anne hem de babaları bulunur. Dişiler genelde işçi olurlar ama bazıları arı sütü ile beslenerek kraliçe olurlar ve yeni bir koloni kurmak üzere kovandan ayrılırlar.
Labels:
altın oran,
fibonacci,
plus magazine
20 Mart 2017
Muhteşem Fibonacci
 Arılar yapıyor, tavşanlar yapıyor ve çok şükür biz insanlar da yapıyoruz: meşhur Fibonacci dizisini (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...) keşfediyoruz.
Arılar yapıyor, tavşanlar yapıyor ve çok şükür biz insanlar da yapıyoruz: meşhur Fibonacci dizisini (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...) keşfediyoruz.İlk olarak 12. yüzyılda Leonardo Fibonacci tarafından yavru tavşanlarla ilgili bir problemi çalışırken bulundu. Sonrasında ayçiçeklerindeki spirallerden arıların aile ağaçlarına kadar doğanın her köşesinde izlerine rastlandı. Bu dizinin önemi altın oran dene sayı ile olan ilişkisinden gelir. Altın oran ise matematiksel özelliklerinin ilginçliği ve güzellik anlayışımızla olan ilgisinden dolayı dikkat çekicidir.
Fibonacci dizisi en önemli sayı dizilerinden biridir. Yukarıda ilk terimleri verilen Fibonacci dizisi aslında ilk iki terimi 1 olan ve sonraki termleri önceki iki terimin toplamı olan dizi şeklinde tarif edilir:
2 = 1 + 1
3 = 1 + 2
5 = 2 + 3
8 = 3 + 5
...
Yani Fibonacci dizisinin sonsuz kadar olan terimlerini tahmin etmek oldukça kolaydır! Yukarıdaki Fibonacci dizisinde bir sonraki terim 55+89=144 olacaktır.
Labels:
altın oran,
dizi,
fibonacci,
plus magazine,
tavşanlar
Kaydol:
Kayıtlar (Atom)